In Deep Learning, data is the most pivotal element and it comes in different formats such as images, text, etc. It is in these simple or complex formats that data needs to be converted to numeric(tensors) for easy interpretation, and storage and ultimately feeding it into a model that can be useful in our day-to-day activities. The purpose of the whole article is poised to give a basic understanding of some of the parameters, what they do and how they work. The article is divided into three segments and be sure to follow all segments in order to get a full comprehension piece by piece.
What are tensors
Tensors are data structures that comprise of scalars, vectors, and matrices of higher dimensions. A single-dimensional tensor can be represented as a vector while a two-dimensional tensor can be represented as a matrix (see the image below).
source: Deep Learning with PyTorch
Even though we can refer to tensors as a multi-dimensional matrix, it is important to note that tensors are dynamic. This means that they have the ability to transform when performing mathematical operations.
Why Tensors Not Numpy Arrays
Numpy is a python library that performs advanced mathematical computations and is very popular in providing multidimensional arrays. Although tensors operate the same way as NumPy arrays, tensors have the ability to perform faster computations on graphical processing units(GPU) becoming the most commonly used data structure in Deep Learning. Another advantage of tensors is that they are immutable, meaning that they can be implemented in several different ways without any change in behavior. Tensors also provide low-level implementations on numerical data structures, which boosts performance and efficiency, unlike Numpy arrays.
Dimensions
Before we proceed to talk about how tensors are stored in memory, we have mentioned that tensors are multidimensional matrices. This leads to the question of what is a dimension. Basically, a dimension is an aspect/detail of something. The purpose of dimensions is to give in-depth details of our data and the more data we have the better but just as Mark Twain said too much of anything is bad, this also applies to our case as well. Let's take for instance a greyscale image, which is represented by a collection of scalars arranged in a grid with height and width(pixels) this automatically equates to a two-dimension H + W. If we add an RGB (Red, Blue, and Green) color channel to our dimension H + W + C, this adds more detail to the image and provides the necessary data to be captured but if we add another 4th dimension, the very essence of the image becomes vague. ln as much as we connote the fact that the more dimensions we have, the more data captured, it is therefore imperative to be able to derive details that are deemed necessary to avoid wastage of resources. ln, a nutshell dimensions play a pivotal role when it comes to tensors and data as a whole.
Storage
Each tensor has a storage property assigned to it that holds data. Let's look at what storage is and how tensors are stored. Storage is a one-dimensional array that contains values of any given data type. For values to be indexed in storage, they have to be allocated in contiguous chunks. This means that the neighboring values/elements are next to each other in memory. Since we mostly work with large dimensional data, how then do we store multi-dimensional matrices in memory when storage is only in one dimension? There are various ways to tackle this paradox but one simple way to approach this is by using Stride. Stride is an indexing method that indicates the number of elements that should be skipped over in storage in order to get to the next element of a given dimension. That's a lot to take in but let's take an example whereby we have a 3 by 3 tensor. We go to the first index on the first row and get all the elements, repeat the same process on the second row and finally the third. By the end of the process, the stride of this dimension will now be a 3 by 1 tensor. In simple terms whenever we call stride, we count the rows and collapse the columns. see the example below.
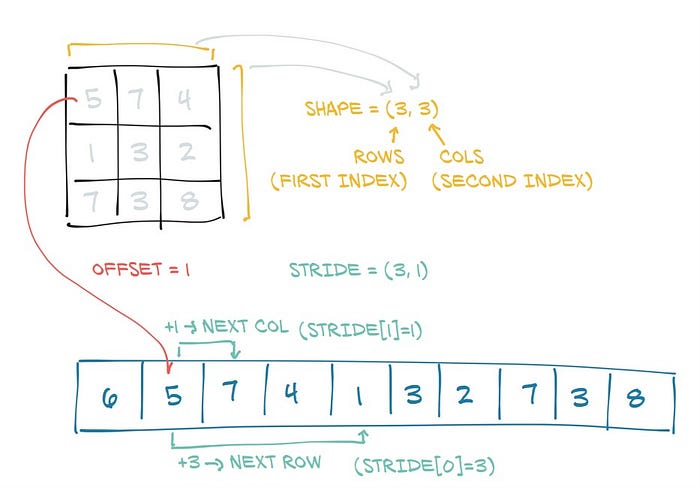source: Deep Learning with PyTorch
Why 32-Bit floating point numbers are the preferred data type for tensors
There are different data types used in tensors, mainly integers, and floating points. Now that we have seen how tensors are stored, let's talk about why use floating point numbers more than integers. Deep Learning involves processing thousands and hundreds of dimensional data, imagine the amount of computational time and memory needed to store all this information. This is why Pytorch tensors have a default data type of 32-bit float which take less computing time and less memory storage. Using these floating numbers improves model accuracy, and increases performance and efficiency. Whenever you hear about deep learning, think of floating point tensors.
Batch Size
Batch size is a hyperparameter in machine learning that consists of a number of samples(tensors) that will be passed through the network at an iteration. Let's imagine we have a plate of rice, do we eat the rice in one go? that's almost impossible unless you want to have an upset stomach, the same thing applies to our model we need to feed the data in bits in order to obtain good results. The batch size determines how the model performs and can be utilized by trying different sizes depending on the data size. Let's take for instance we have 10 000 samples of data, we can define the batch size to 100, data will then be grouped and passed to the model as sets of 100. we will later see the impact of batch size
Conclusion
In the next article, we will delve into ways we can convert text data to tensors and also look at some of the most popular tokenization algorithms used in deep learning.